 |
| • | AllPairsTriangles: | All-pairs intersection testing between triangles of two meshes (CPU, GPU). |
| • | IntersectBoxCone: | Test-intersection queries for an aligned/oriented box and a (finite) cone. |
| • | IntersectBoxCylinder: | Test-intersection queries for an aligned/oriented box and a (finite) cylinder. |
| • | IntersectBoxSphere: | Test-intersection queries for an aligned/oriented box and a sphere. |
| • | IntersectConvexPolyhedra: | Find-intersection query for two convex polyhedra. |
| • | IntersectCylinders: | Test-intersection queries for two finite cylinders. |
| • | IntersectInfiniteCylinders: | Find-intersection query for two infinite cylinders. The curve of intersection is computed. |
| • | IntersectLineRectangle: | Find-intersection and test-intersection queries for a line, ray, or segment and a rectangle. |
| • | IntersectLineTorus: | Find-intersection query for a line and a torus. |
| • | IntersectPlaneConvexPolyhedron: | Find-intersection query for a plane and a convex polyhedron. |
| • | IntersectSphereCone: | Test-intersection queries for a sphere and a cone (infinite cone, infinite truncated cone, finite cone, cone frustum). |
| • | IntersectTriangleBox: | Determine whether a triangle and an oriented box intersect. |
| • | IntersectTriangleCylinder: | Determine whether a triangle and a cylinder intersect. |
| • | IntersectTriangles2D: | Test-intersection and find-intersection queries for two triangles in 2D. |
| • | MovingCircleRectangle: | Illustration of computing first time and point of contact between moving circles and rectangles. |
| • | MovingSphereBox: | Illustration of computing first time and point of contact between moving spheres and boxes. |
| • | MovingSphereTriangle: | Illustration of computing first time and point of contact between moving spheres and triangles. |
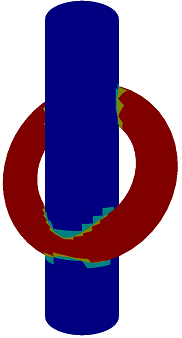
AllPairsTriangles. All-pairs comparison of triangles between two meshes to detect intersecting triangles.
The code uses GPGPU for the triangle-triangle intersection testing. The same algorithm
is implemented on the CPU to give you an idea of how much faster the GPGPU version is.
The cylinder has 4416 triangles and the torus has 4608 triangles. The all-pairs
test-intersection queries on the GPU run at 170 frames per second on an AMD 7970.
The cylinder triangles that do not intersect torus triangles are dark blue; those
that do are cyan. The torus triangles that do not intersect cylinder triangles
are red; those that do are gold. The CPU version is better measured in terms of
seconds per frame. The application fps display shows 0.0. Whether CPU or GPU,
a bounding-volume hierarchy can be used to localize the intersection testing.
On the GPU, append-consume buffers may be used to store results. Also, the
GPU version can be modified to compute actual line segments or points of
intersection.
|
IntersectBoxCone. Determine whether an oriented box and a cone intersect in the context of
culling. The prototypical case is when the cone represents a spot light
and lighting of objects is expensive. The oriented box is a bounding box
for an object. If the bounding box does not intersect the cone, the object
need not be lit; thus, the object is culled from the lighting pass. If the
light is not attenuated, the cone is chosen to be infinite and the box-cone
intersection test is always correct. However, if the light is not attenuated
and the extent of the light's influence is modeled by using a finite cone
(infinite cone truncated by a plane perpendicular to the cone axis), then
the box-cone intersection test is conservative and can have false
positives. It is possible that the query reports an intersection when there
is none. In particular, this happens when a portion of the box is inside
the infinite cone but above the truncating plane but another portion of
the box is below the truncating plane (see the images below). The application
is dynamic, allowing you to translate and rotate the box using the keyboard.
The box is drawn in red when it intersects the cone or drawn in blue when it
does not intersect the cone.
Top-left: The initial configuration where the cone vertex is inside the box (intersection).
Top-middle: The cone vertex is not in the box and all box vertices and edges
are outside the cone, but the cone passes through box faces (intersection).
Top-right: The box is outside the cone with one edge close to the cone (no intersection).
Bottom-left: The box in the top-right is moved closer to the cone. A box
edge intersects the cone but the edge endpoints are outside the cone (intersection).
Bottom-middle: The box is above the truncating plane of the cone (no intersection).
Bottom-right: A false positive. The box straddles the truncating plane and
straddles the cone boundary. The query reports an intersection when there is not one.
This is akin to plane-at-a-time box-frustum culling for visibility testing. If a box
is outside any frustum plane, it is not visible; otherwise, draw the box. It is possible
the box straddles two frustum planes--not outside either plane--yet the box does not
intersect the frustum.
|
IntersectBoxCylinder. Test-intersection queries for an aligned/oriented box and a (finite) cylinder.
The implementation uses the algorithm described in the PDF mentioned below.
Two views of an intersection between a box and a cylinder.
|
IntersectBoxSphere. Test-intersection queries for an aligned/oriented box and a sphere. The
manipulation of objects is similar to that of the box-cone application.
Left: The box and sphere intersect. Right: The box and sphere do not intersect.
|
IntersectConvexPolyhedra. Find-intersection query for two convex polyhedra. The sample computes two meshes that
approximate ellipsoids, allows you to rotate them and then computes the mesh of the
intersection of the polyhedra.
Four intersection configurations are shown next.
|
IntersectCylinders. Test-intersection queries for two finite cylinders.
Two intersection configurations are shown. When the cylinders are not
intersecting, they are drawn in red and blue. When the cylinders are
intersectin, they are drawn in magenta and cyan. Each cylinder can be
rotated or translated, the cylinder selection using the '0' or '1' keys.
Translations are obtained by the 'x', 'X', 'y', 'Y', 'z' or 'Z' keys.
Rotations are obtained by the 'p', 'P', 'r' or 'R' keys.
|
IntersectInfiniteCylinders. Find-intersection query for two infinite cylinders. The curve of intersection is computed.
One intersection configuration is shown next. The cylinders are drawn in red and
blue wireframes. The curve of intersect is drawn as a green polyline.
|
IntersectLineRectangle. Find-intersection and test-intersection queries for a line, ray, or segment and a rectangle.
The code has conditional compilation for you to choose queries involving lines, rays
or segments. The find-intersection query is used to compute a point of intersection
(if any). The test-intersection query intersection Boolean is compared to that of
the find-intersection query, throwing an exception if they do not match. The 2x3 array
of images show line, ray, and segment left-to-right. The first row shows an intersection
result and the second row shows a no-intersection result. You can translate and rotate
the rectangle and visualize using a virtual trackball.
|
IntersectLineTorus. Find-intersection query for a line and a torus.
The left image shows the initial configuration. The line always contains the camera
position (eyepoint) and is initially in the view direction, so the line is not visible.
To generate a new line, right-click with the mouse at a point. The line contains the
eyepoint and the selected point (in world space) as is done with the graphics picking
system. The middle image shows the first point of intersection along the line, and it
is drawn as a small black sphere. Rotate the scene using left-click-drag of the mouse
to obtain the right image. Now the line is visible and any points of intersection are
drawn as small black spheres. Wireframe is used so that you can see all 4 points of
intersection.
The scene is rotated via the trackball using left-click-drag of the mouse. A right-click of the mouse selects a point on the torus, as is shown in the left image. Rotating the scene again allows you to see the line and the 2 points of intersection.
|
|
IntersectPlaneConvexPolyhedron. Find-intersection query for a
plane and a convex polyhedron.
Two intersection configurations are shown. All objects are drawn with
semitransparency. The plane is drawn in gray. The portion of the convex
polyhedron on the positive side of the plane is drawn in red. The portion
of the convex polyhedron on the negative side of the plane is drawn in
blue. The convex polygon of intersection of the plane and convex polyhedron
is drawn in green. The plane can be translated in its normal direction using
the '-' or '+' keys. The convex polyhedron can be rotated using the 'a', 'A',
'b' or 'B' keys. The objects can be drawn in wireframe mode, toggled by the
'w' or 'W' keys, which shows the topological complexity of the subpolyhedra.
The left image is the initial configuration. The right image shows the plane moved in its negative normal direction and the polyhedron rotated.
You can also toggle drawing of each object. The left image has the positive polyhedra turned off (toggle with 'p' or 'P'). The middle image has the negative polyhedra turned off (toggle with 'n' or 'N'). The right image has the solid polygon of intersection turned off (toggle with 'm' or 'M).
The left image has the solid polygon drawn in green with a black boundary curve. The right image has the boundary curve turned off (toggle with 'c' or 'C').
|
IntersectSphereCone. Test-intersection queries for a sphere and a cone (infinite cone, infinite truncated cone,
finite cone, cone frustum). The manipulation of objects is similar to that of the
box-cone application.
Various configurations are shown next. The sphere is drawn in red. The cone wall is
drawn in blue and the cone disk caps are drawn in green when the cone and sphere are
not intersecting. The cone wall is drawn in cyan and the cone disk caps are drawn in
yellow when the cone and sphere are intersecting.
|
IntersectTriangleBox. Determine whether a triangle and an oriented box intersect. The test-intersection
query uses the method of separating axes. The find-intersection query clips the
triangle against the planes of the box faces.
Left: The box and triangle intersect. Right: The box and triangle do not intersect.
|
IntersectTriangleCylinder. Determine whether a triangle and a cylinder intersect.
Upper-left: The triangle and cylinder do not intersect initialy.
Upper-middle: The triangle is rotated about its center with the r-key several times until the triangle and cylinder intersect.
Upper-right: Wireframe view of the upper-middle configuration.
Lower-left: The triangle is rotated about is center until it is nearly intersecting the cylinder.
Lower-middle: The triangle is rotated slightly more so that it is intersecting the cylinder.
|
IntersectTriangles2D. Test-intersection and find-intersection queries for two triangles in 2D.
Left: Test-intersection query, the triangles do not intersect.
Middle: Test-intersection query, the triangles overlap.
Right: Find-intersection query, the triangles intersect and the overlap is drawn in gray.
|
MovingCircleRectangle. Illustration of computing first time and point of contact between moving circles and rectangles.
For a specified stationary rectangle, the query is performed for a moving
circle. The rectangle is drawn as a blue wireframe. The rounded rectangle
is drawn as a light-gray region. The circle is drawn as a red wireframe.
The velocity vector has unit length in this application. The ray whose
origin is the circle center and with the velocity as direction is drawn in
green. Two rays tangent to the circle and parallel to the velocity are
drawn to that you can see where they intersect the rounded rectangle.
You can left-click-and-drag the mouse to modify the velocity vector. You
can right-click-and-drag the mouse to move the circle center. If you
press the [+] key, the rectangle is rotated clockwise. If you press the
[-] key, the rectangle is rotated counterclockwise. The left image shows a
screen capture where the circle and rectangle are not initially overlapping
but intersect at a later time. The right image shows a screen capture where
the circle and rectangleare initially overlapping. Some point is chosen
as the contact point even though the intersection point set has positive area.
|
MovingSphereBox. Illustration of computing first time and point of contact between moving spheres and boxes.
For a specified stationary box, the query is performed for a moving sphere.
The box and rounded box are drawn semitransparently. The query sphere is drawn
in light gray. When there is a first contact time and point, a dark gray sphere
is drawn to indicate where the light gray sphere moves to achieve first contact.
The contact point is drawn as a small red sphere. The ray C+tV is drawn as a
line segment. You can change the velocity V by pressing 'a' and 'b' keys (modifies
angles in spherical coordinates). The sphere can be translated using 'x', 'y'
and 'z' keys.' The images show a couple of contact configurations. The 3-tuples
of numbers in the upper-left of the images are the contact points.
|
MovingSphereTriangle. Illustration of computing first time and point of contact between moving spheres and triangles.
For a specified stationary triangle, the query is performed for a moving sphere.
The triangle and sphere-swept volue are drawn semitransparently. The query sphere is drawn
in light gray. When there is a first contact time and point, a dark gray sphere
is drawn to indicate where the light gray sphere moves to achieve first contact.
The contact point is drawn as a small black sphere. The ray C+tV is drawn as a
green line segment. You can change the velocity V by pressing 'a' and 'b' keys (modifies
angles in spherical coordinates). The sphere can be translated using 'x', 'y'
and 'z' keys.' The images show three contact configurations, one with a triangular face,
one with a half cylinder and one with a sphere wedge. The numbers in the upper-left of
the images are the contact times and contact points.
|