 |
 |
 |
| • | DistanceAlignedBoxes: | Robust computation of distance between aligned boxes in any dimension. |
| • | DistanceAlignedBoxOrientedBox: | Robust computation of distance between an aligned box and an oriented box in dimension 3. |
| • | DistanceOrientedBoxes: | Robust computation of distance between oriented boxes in dimension 3. |
| • | DistancePointConvexPolyhedron: | Robust computation of distance between a point and a convex polyhedron in dimension 3. |
| • | DistancePointHyperellipsoid: | Robust computation of distance between a point and an ellipse (2D) or ellipsoid (3D) or hyperellipsoid (any dimension). |
| • | DistanceRectangleBox: | Robust computation of distance between a rectangle and an aligned or oriented box in dimension 3. |
| • | DistanceSegments3: | Robust computation of distance between line segments in any dimension (CPU and GPU). |
| • | DistanceTriangleBox: | Robust computation of distance between a triangle and an aligned or oriented box in dimension 3. |
DistanceAlignedBoxes. Robust computation of distance between aligned boxes in any dimension.
The algorithm is based on convex quadratic programming (CQP) and a
formulation as a linear complementarity problem (LCP).
Various configurations are shown next.
|
DistanceAlignedBoxOrientedBox. Robust computation of distance between an aligned box and an oriented box
in dimension 3. The algorithm is based on convex quadratic programming (CQP)
and a formulation as a linear complementarity problem (LCP).
Various configurations are shown next.
|
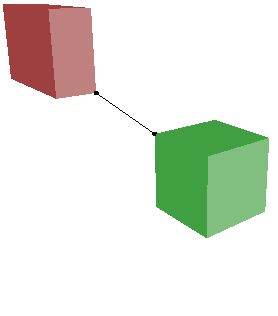
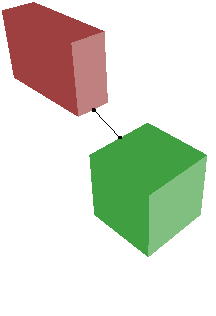
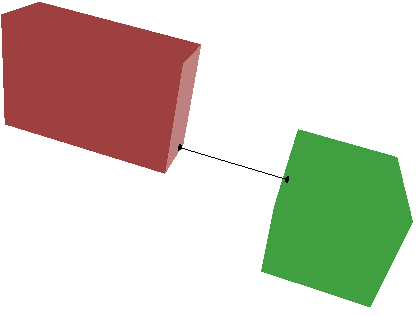
DistanceOrientedBoxes. Robust computation of distance between oriented boxes in dimension 3.
The algorithm is based on convex quadratic programming (CQP) and a
formulation as a linear complementarity problem (LCP).
Various configurations are shown next. The right-most configuration shows the
two boxes overlapping. The distance is zero, but the convex polyhedron of
intersection is not computed.
|
DistancePointConvexPolyhedron. Robust computation of distance between a point and a convex polyhedron in dimension 3.
The algorithm is based on convex quadratic programming (CQP) and a
formulation as a linear complementarity problem (LCP).
Various configurations are shown next. The point is drawn as the center of the
green sphere. The left configuration has a face point as closest point. The
middle configuration has an edge point as closest point. The right configuration
has a vertex as closest point.
|
| DistancePointHyperellipsoid. Robust computation of distance between a point and an ellipse (2D) or ellipsoid (3D) or hyperellipsoid (any dimension). This is a simple test program to verify the distances. |
DistanceRectangleBox. Robust computation of distance between a rectangle and an aligned box or an oriented box in dimension 3.
The algorithm is based on convex quadratic programming (CQP) and a
formulation as a linear complementarity problem (LCP).
Two configurations are shown next.
|
| DistanceSegments3. Robust computation of distance between line segments in any dimension (CPU and GPU). The sample has accuracy and performance tests, both for the CPU and GPU. The performance test involves all-pairs distance computations for a large number of pairs of segments in 3D. |
DistanceTriangleBox. Robust computation of distance between a triangle and an aligned box or an oriented box in dimension 3.
The algorithm is based on convex quadratic programming (CQP) and a
formulation as a linear complementarity problem (LCP).
Two configurations are shown next.
|
